Statistics: Difference between revisions
Jump to navigation
Jump to search
| Line 11: | Line 11: | ||
* population mean <math>\mu</math> is the average over the entire population of size N <math>\mu = \frac{1}{N}\sum^N x_i</math> | * population mean <math>\mu</math> is the average over the entire population of size N <math>\mu = \frac{1}{N}\sum^N x_i</math> | ||
* sample mean <math>\overline{x}</math> is the average over a sample of size n (usually n << N) <math>\overline{x} = \frac{1}{n}\sum^n x_i</math> | * sample mean <math>\overline{x}</math> is the average over a sample of size n (usually n << N) <math>\overline{x} = \frac{1}{n}\sum^n x_i</math> | ||
==Variance and Standard Deviation== | ==Variance and Standard Deviation== | ||
Latest revision as of 00:46, 10 December 2013
from Biostatistics, by Paulson 2008
Normal Distribution
- 68% of area lies within one standard deviation of the mean
- 95% for two
- 99.7% for three standard deviations
Mean
- population mean <math>\mu</math> is the average over the entire population of size N <math>\mu = \frac{1}{N}\sum^N x_i</math>
- sample mean <math>\overline{x}</math> is the average over a sample of size n (usually n << N) <math>\overline{x} = \frac{1}{n}\sum^n x_i</math>
Variance and Standard Deviation
- population variance <math>\sigma^2 = \frac{1}{N}\sum (x_i-\mu)^2</math>
- sample variance <math>s^2 = \frac{1}{n-1}\sum (x_i-\overline{x})^2 = \frac{\sum x_i^2 -n\overline{x}^2}{n-1} </math>
- standard deviation is the square root of variance
Mode, Median
- The mode of a sample is simply the value that occurs most often
- The median is the value that has an equal number of values above and below it. If there are an even number of values, you average the two middle ones.
Z and Student's t Distribution
- Z distribution for a sample normalizes <math>z_i = \frac{x_i-\overline{x}}{s}</math>
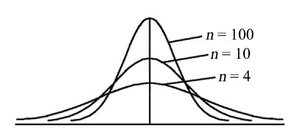
- Student's t distribution approximates z distribution but compensates for smaller samples by fattening tails as n gets smaller. It is essentially standard normal for n > 100. The parameter is called "degrees of freedom", and amounts to n-1
Standard Error of the Mean, or Mean Standard Error (MSE)
- <math>s_{\overline{x}} = \frac{s}{\sqrt{n}}</math>
- standard deviationof the sample: 95% of sample values lie within the interval <math>\overline{x} \pm 2s</math>
- standard deviation of the mean: the true mean <math>\mu</math> lies within the interval <math>\overline{x} \pm 2s_{\overline{x}}</math> 95% of the time
- In statistical tests, the means of samples are compared, not the data points themselves
Confidence Intervals
The interval <math>\overline{x} \pm t(\alpha/2, n-1) \frac{s}{\sqrt{n}}</math> contains the mean <math>\mu</math> with a confidence level of <math>1-\alpha</math>. For example, <math>\alpha</math> would be 0.05 for a 95% confidence interval.
Hypothesis testing
- Upper-tail test: Does sample A have higher values than sample B? We look at A - B > 0
- Lower-tail test: Does sample A have lower values than sample B? We look at A - B < 0
- Two-tail test: Is sample A different from sample B? We look at A - B not equal to zero
- In all cases, the null hypothesis is that A - B is equivalent to zero within the accuracy of our test.
- A - B is represented by z or t values, and tails refer to the outlying values of the standard normal or t distribution.
- The two tail test is more general, but the upper and lower tail tests are more powerful because they are more specific.
- Rejecting the null hypothesis is significant, but failing to reject it is not.
Two types of errors
- Type 1 error: alpha is the probability (or "acceptance level") of rejecting the null hypothesis when you shouldn't. So if <math>\alpha = 0.05</math>, we will falsely claim a significant difference 5 times out of 100.
- Type 2 error: beta is the probability (or "acceptance level") of sticking with the null hypothesis when you shouldn't. So if <math>\beta = 0.20</math>, we will wrongly ignore a significant different 20 times out of 100.
- The power of the statistic is defined as <math>1-\beta</math>
Compare one sample to a known standard value
- Calculated t value is
<math>t_c = \frac{\overline{x}-c}{s/\sqrt{n}}</math>
where c is known standard value. Note that this is close to zero if the mean is close to the known standard value.
- Two-tail test: Null hypothesis is that<math>t(-\alpha/2, n-1) < t_c < t(\alpha/2, n-1)</math>Rejection means that our mean is significantly different from the standard value.
- Lower-tail test: Null hypothesis is that<math>t_c > t(-\alpha, n-1)</math>Rejection means that our mean is significantly less than the standard value.
- Upper-tail test: Null hypothesis is that<math>t_c < t(\alpha, n-1)</math>Rejection means that our mean is significantly greater than the standard value.
Determining adequate sample size for one-sample test
- Rough estimate:<math>n \ge \frac{z_{\alpha/2}^2s^2}{d^2}</math>where s is an estimate of deviation and d is "detection level", the minimum difference from the standard value that needs to be detected
- Iterative method:<math>n \ge \frac{t^2(\alpha/2, n-1)s^2}{d^2}</math>Here, n shows up on both sides of the equation, so start with a large estimate of n and recalculate until it converges.
Two-sample independent t test
- Assume that each sample comes from a normal distribution
- We can make no assumptions about the variances of the two samples
- Calculated test statistic is<math>t_c = (\overline{x}_A-\overline{x}_B)/\sqrt{\frac{s_A^2}{n_A}+\frac{s_B^2}{n_B}}</math> with <math>n_1+n_2-2</math> degrees of freedom
- Sample size determination:<math>n \ge \frac{(s_1^2+s_2^2)(z_{\alpha/2}+z_{\beta})^2}{d^2}</math>
Two-sample pooled t test
- Assume that each sample comes from a normal distribution
- Assume that variances of the two samples are close to equal
- Pooled standard deviation is<math>s_{pooled} = \sqrt{\frac{(n_A-1)s_A^2+(n_B-1)s_B^2}{n_A+n_B-2}}\sqrt{\frac{1}{n_A}+\frac{1}{n_B}}</math>
- Calculated test statistic is<math>t_c = \frac{\overline{x}_A - \overline{x}_B}{s_{pooled}}</math>
- Sample size determination:<math>n \ge \frac{s_{pooled}^2(z_{\alpha/2}+z_{\beta})^2}{d^2}</math>
Paired t test
- Assume that each sample comes from a normal distribution
- Samples come in pairs (e.g. each test subject is matched to an otherwise identical control)
- We do statistics on <math>d = x_A-x_B</math>
- Mean(n is the number of pairs!):<math>\overline{d} = \frac{1}{n}\sum{(x_A-x_B)} = \frac{1}{n}\sum{d}</math>
- Standard deviation of pair differences is<math>s_{paired} = \sqrt{\frac{\sum{(d_i-\overline{d})^2}}{n-1}}</math>
- Test statistic:<math>t_c = \frac{\overline{d}\sqrt{n}}{s_{paired}}</math>
- Sample size determination:<math>n \ge \frac{s_{paired}^2(z_{\alpha/2}+z_{\beta})^2}{d^2}</math>
Two boolean sample proportion t test
- If each trial is a boolean "success" or "failure", let P denote the proportion of successes for the sample.
- The combined proportion of samples A and B is<math>P_c = \frac{n_A P_A+n_B P_B}{n_A+n_B}</math>
- The sample standard deviation is<math>s = \sqrt\frac{P_c(1-P_c)}{n_A+n_B}</math>
- The test statistic is<math>t_c = \frac{P_A - P_B}{s}</math>
One-factor ANOVA
- This is analogous to a two-sample independent t-test, but with more than two samples.
- We assume that the sampled populations are normally distributed with different means but the same variance.
- Let <math>j = 1 ... m</math> denote the m different populations, and <math>i = 1 ... n</math> denote the n members <math>x_{ij}</math> in each sample.
- Let <math>\overline{x}_j = \frac{1}{n}\sum_{i=1}^n x_{ij}</math> denote the mean of the jth sample, and let <math>\overline{\overline{x}} = \frac{1}{nm}\sum_i \sum_j x_{ij} = \frac{1}{m}\sum_{j=1}^m\overline{x}_j</math> denote the mean of all the samples.
- The sample variance of the population means (also "mean square treatment") is<math>MST = \frac{1}{m-1}\sum_j(\overline{x}_j - \overline{\overline{x}})^2</math>
- The mean of the sample variances (also "mean square error") is<math>MSE = \frac{1}{m(n-1)}\sum_i \sum_j(x_{ij} - \overline{x}_j)^2</math>
- The test statistic is <math>F_c = \frac{MST}{MSE}</math>
- The null hypothesis is that the populations are not significantly different from each other, so that <math>F_c \approx 1</math>.
- We reject the null hypothesis at level alpha if <math>F_c > F_t = F[\alpha, m-1, m(n-1)</math>], where
- <math>F(\alpha, d_1, d_2)</math> is F-test based on the Fisher or F-distribution. See http://en.wikipedia.org/wiki/F-test
Contrasts (Tukey method)
- http://en.wikipedia.org/wiki/Tukey%27s_test
- Make the same assumptions as in one-factor ANOVA above, but instead of testing everything all at once, we compare each pair of populations independently.
- For each pair of means, we reject the null hypothesis (that they are the same) if<math>|\overline{x}_i - \overline{x}_j| > q(\alpha, m, m(n-1))\sqrt{\frac{MSE}{n}}</math>, where <math>q(\alpha, d_1, d_2)</math> is based on a Tukey-Cramer distribution.
Confidence Intervals
- We can also compare confidence intervals for each population:<math>\mu_i = \overline{x}_i \pm t(\alpha/2, m(n-1))\sqrt{\frac{MSE}{n}}</math>
Sample size estimate
<math>n \ge \frac{m\cdot MSE(z_{\alpha/2}+z_\beta)^2}{\delta^2}</math>, where the MSE is estimated beforehand and delta is the desired detection level
Blocked ANOVA
- This is like the paired t-test for more than two populations.
- We assume that the sampled populations are normally distributed with different means but the same variance.
- We further assume that samples come in blocks, each member of the blocks coming from one of each population.
- Let <math>j = 1 ... m</math> denote the m different populations, and <math>i = 1 ... n</math> denote the n groups of members <math>x_{ij}</math> in each sample.
- In addition to the notation above, let<math>\overline{x}_i = \frac{1}{m}\sum_{j=1}^m x_{ij}</math> denote the mean of the ith block.
- The sample variance of the population means (also "mean square treatment") is<math>MST = \frac{n}{m-1}\sum_j(\overline{x}_j - \overline{\overline{x}})^2</math>
- The sample variance of the block means (also "mean square block") is<math>MSB = \frac{m}{n-1}\sum_i(\overline{x}_i - \overline{\overline{x}})^2</math>
- The mean of the sample variances (also "mean square error") is<math>MSE = \frac{1}{(m-1)(n-1)}\sum_i \sum_j(x_{ij} - \overline{x}_j)^2</math>
- There are two null hypotheses and two statistics:
- Reject the hypothesis that the populations share the same mean if<math>\frac{MST}{MSE} > F[\alpha, m-1, (m-1)(n-1)</math>]
- Reject the hypothesis that the blocks share the same mean if<math>\frac{MSB}{MSE} > F[\alpha, n-1, (m-1)(n-1)</math>]
- If the blocks turn out to be the same, you gain no power by choosing the blocked ANOVA over the standard one-way ANOVA.
Contrasts (Tukey method)[1]
- Make the same assumptions as in blocked ANOVA above, but instead of testing everything all at once, we compare each pair of populations independently.
- For each pair of means, we reject the null hypothesis (that they are the same) if<math>|\overline{x}_i - \overline{x}_j| > q(\alpha, m, (m-1)(n-1))\sqrt{\frac{MSE}{n}}</math>, where <math>q(\alpha, d_1, d_2)</math> is based on a Tukey-Cramer distribution.
Confidence Intervals
- We can also compare confidence intervals for each population:<math>\mu_i = \overline{x}_i \pm t(\alpha/2, (m-1)(n-1))\sqrt{\frac{MSE}{n}}</math>
Sample size estimate
<math>n \ge \frac{m\cdot MSE(z_{\alpha/2}+z_\beta)^2}{\delta^2}</math>, where the MSE is estimated beforehand and delta is the desired detection level
Fitting data with least-squares regression
- We have a set of n (x,y) pairs, and want to fit these points to a line <math>\hat{y} = a + bx</math>
- Estimate the slope with<math>b = \frac{\sum{xy} - n\overline{x} \overline{y}}{\sum{x^2} - n\overline{x}^2}</math>
- Estimate the y-intercept with<math>a = \overline{y}-b\overline{x}</math>
Linearizing Data
- Linearize by increasing or decreasing the power of the x or y values, or both. Linearizing y only is most common.
- Here is the sequence of transformations to try:<math>..., y^{-3}, y^{-2}, y^{-1}, y^{-1/2}, \log{y}, y^{1/2}, y, y^2, y^3, ...</math>
Interpolating from the Linear Regression
- Extrapolating beyond the data range is risky.
- After solving for a and b, you can generate an alpha-level confidence interval for the average <math>\hat{y}</math> for a given x:<math>\overline{\hat{y}} \pm t(\alpha/2, n-2)\sqrt{\frac{\sum(y-\hat{y})^2}{n-2}\left[\frac{1}{n}+\frac{(x-\overline{x})^2}{\sum(x-\overline{x})^2}\right]}</math>
Correlation
- For a set of n (x,y) pairs, we can talk about how well the samples are correlated.
- Correlation coefficient is denoted as r:<math>r = \frac{\sum{xy}-\frac{1}{n}\sum{x}\sum{y}}{\sqrt{\left[\sum{x^2}-\frac{1}{n}\left(\sum{x}\right)^2\right]\left[\sum{y^2}-\frac{1}{n}\left(\sum{y}\right)^2\right]}}</math>
- A r = 1 means a perfectly linear relationship with positive slope. r = -1 is perfectly correlated with negative slope. r = 0 means no relationship.
- Coefficient of determination is <math>r^2</math> and has a direct interpretation. If <math>r^2 = 0.9</math>, that means 90% of the data variability can be explained by the regression equation. The rest is random noise.
Testing boolean data
- We have a sample of size n from a population of boolean trials, and we know that proportion p of the trials resulted in success.
- The sample mean is just p, and for the sake of discussion, assume <math>p < 1-p</math>.
- If <math>np > 5</math>, we model the sample as binomial and take the sample variance as <math>s^2 = p(1-p)</math>
- If <math>np \not> 5</math>, we model the sample as Poisson and take the sample variance as <math>s^2 = p</math>
Confidence interval for mean of boolean sample
- The confidence interval for the sample mean is <math>p \pm z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}</math> or <math>p \pm z_{\alpha/2}\sqrt{\frac{p}{n}}</math>
- If p is anywhere near 0.5, we throw in the "Yates factor" to expand the confidence interval:<math>p - z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}} - \frac{1}{2n} < \pi < p + z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}} + \frac{1}{2n}</math>
Comparing the mean of a boolean sample to a standard value
- To compare the mean p to a standard value c, we use as test statistic<math>z_c = \frac{p-c}{\sqrt{\frac{p(1-p)}{n}}}</math> or <math>z_c = \frac{p-c}{\sqrt{\frac{p}{n}}}</math>Note that this is close to zero when p is close to c.
- Two-tail test: Null hypothesis is that<math>-z_{\alpha/2} < z_c < z_{\alpha/2}</math>Rejection means that our mean is significantly different from the standard value.
- Lower-tail test: Null hypothesis is that<math>z_c > -z_{\alpha}</math>Rejection means that our mean is significantly less than the standard value.
- Upper-tail test: Null hypothesis is that<math>z_c < z_\alpha</math>Rejection means that our mean is significantly greater than the standard value.